added cours 25
Showing
- slides/cours_25.md 764 additions, 0 deletionsslides/cours_25.md
- slides/figs/floyd_exemple.png 0 additions, 0 deletionsslides/figs/floyd_exemple.png
- slides/figs/floyd_exercice.png 0 additions, 0 deletionsslides/figs/floyd_exercice.png
- slides/figs/prim_0.png 0 additions, 0 deletionsslides/figs/prim_0.png
- slides/figs/prim_1.png 0 additions, 0 deletionsslides/figs/prim_1.png
- slides/figs/prim_2.png 0 additions, 0 deletionsslides/figs/prim_2.png
- slides/figs/prim_3.png 0 additions, 0 deletionsslides/figs/prim_3.png
- slides/figs/prim_4.png 0 additions, 0 deletionsslides/figs/prim_4.png
- slides/figs/prim_5.png 0 additions, 0 deletionsslides/figs/prim_5.png
- slides/figs/prim_exercice.png 0 additions, 0 deletionsslides/figs/prim_exercice.png
- slides/figs/prim_solution.png 0 additions, 0 deletionsslides/figs/prim_solution.png
slides/cours_25.md
0 → 100644
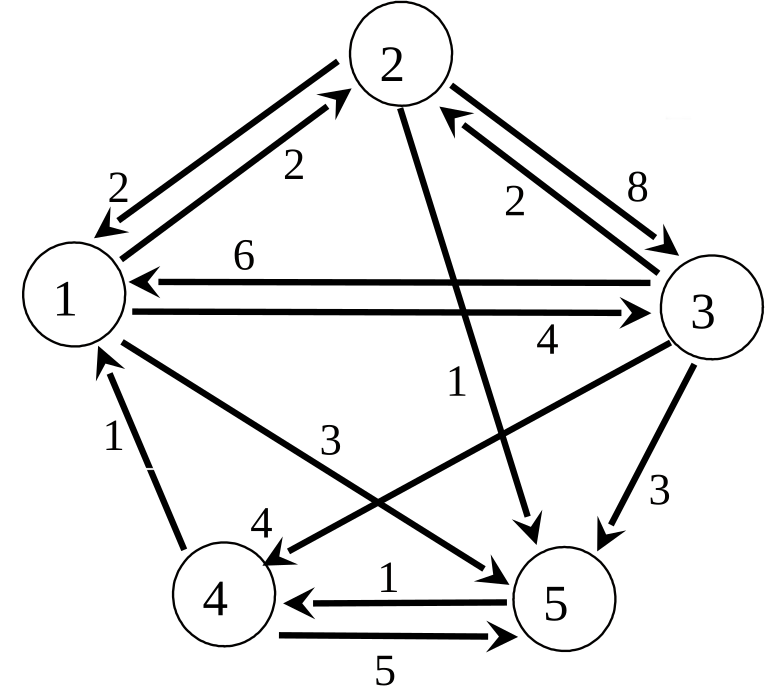
slides/figs/floyd_exemple.png
0 → 100644
82.7 KiB
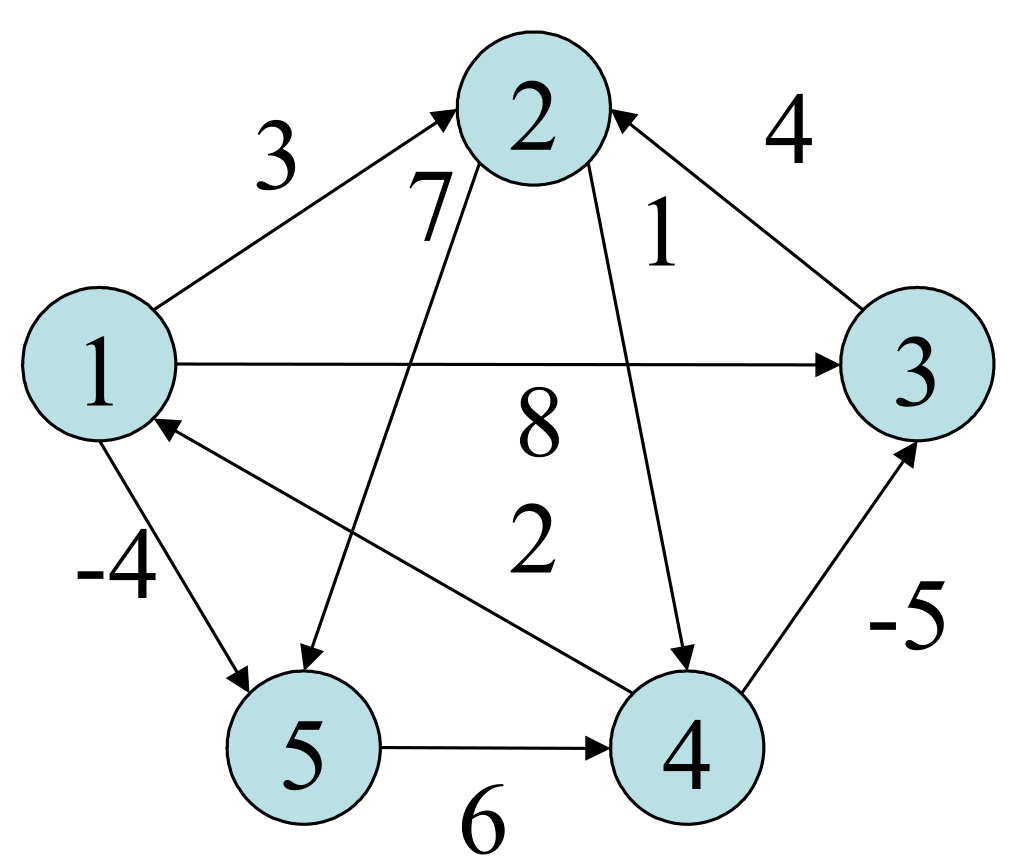
slides/figs/floyd_exercice.png
0 → 100644
91.4 KiB
slides/figs/prim_0.png
0 → 100644
37.3 KiB
slides/figs/prim_1.png
0 → 100644
37.7 KiB
slides/figs/prim_2.png
0 → 100644
37.7 KiB
slides/figs/prim_3.png
0 → 100644
38.1 KiB
slides/figs/prim_4.png
0 → 100644
38.6 KiB
slides/figs/prim_5.png
0 → 100644
39.3 KiB
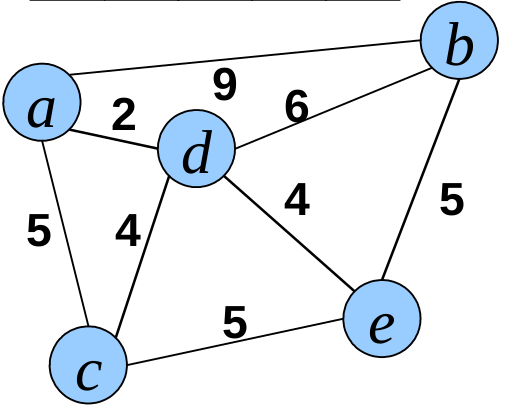
slides/figs/prim_exercice.png
0 → 100644
53.2 KiB
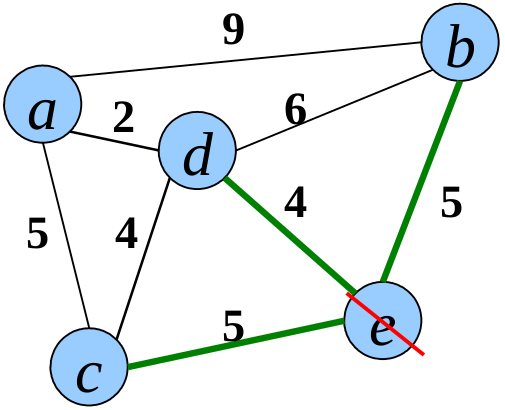
slides/figs/prim_solution.png
0 → 100644
101 KiB